LA CUEILLETTE DES OLIVES ...
ET L'ATTERRISSAGE TOUS TEMPS
par René LAMI
Commandant de Bord à la compagnie Air France
Aucun rapport ? Voire, dirait Panurge... Je me suis laissé dire qu'en Provence, pour chaque olive récoltée, le propriétaire devait payer l'équivalent de trois à ceux qui les cueillent.
Si la récolte coûte si cher, c'est qu'on n'a jamais réussi à créer une machine capable de remplir cette tâche pourtant si facile pour un être humain : saisir l'olive (sans l'écraser !) et la déposer dans un panier. De doctes personnages sauraient, avec les mots hermético-scientifiques adéquats, expliquer les subtils mécanismes de l'apprentissage des gestes élémentaires au cours de la petite enfance,
Pour ma part, je me contenterai de faire observer que tout être humain normalement constitué accomplit quotidiennement une foule de tâches parfois très complexes, avec une précision, une régularité et une sûreté supérieures à celles des machines les plus raffinées et les plus " fiables ". On sait, en particulier, que les réflexes d'équilibre, acquis souvent bien après l'âge tendre, sont définitifs : par exemple nul n'éprouve d'appréhension à remonter sur une bicyclette après de nombreuses années d'interruption, même quand le souffle et la résistance musculaire ont disparu.
Personne, sans doute, n'en est surpris. Mais il est étonnant que l'on n'ait pas cherché à exploiter ces merveilleuses facultés humaines et à réunir les conditions nécessaires à leur utilisation.
Si, au lieu de fournir à l'homme qui cueille les olives une échelle, un panier... et la vue directe de l'olive, on lui donnait une pince qu'il ne verrait pas, mais dont il connaîtrait les écarts à l'olive selon trois directions indiquées sur trois cadrans, il y a fort à parier que la culture de l'olivier disparaîtrait définitivement.
C'est pourtant un peu ce qui se passe quand le pilote est privé de visibilité extérieure : il était habitué à juger ses mouvements par l'observation du dé placement relatif de l'image du monde extérieur. D'autre part, en dirigeant son avion vers une piste, il estimait sa position et élaborait sa trajectoire selon la façon dont il voyait cette piste. Privé de visibilité extérieure, il doit juger ses déplacements d'après des mouvements d'aiguilles, index ou cadrans se déplaçant de quantités très faibles, et de façon complètement différente de l'image extérieure
Le pilotage " aux fesses ".
Aux débuts de l'aviation, on avait cru longtemps à l'importance des sensations d'équilibre : ce que l'on appelait dans le jargon familier le " pilotage aux fesses "... jusqu'au jour où l'on s'aperçut que les meilleurs pilotes, privés de visibilité extérieure, se mettaient dans les positions les plus invraisemblables.
Il fallut se rendre à l'évidence : les sensations d'équilibre, perturbées par les accélérations de la trajectoire décrite, devenaient inutilisables et même nuisibles.
C'était donc surtout l'observation du mouvement relatif de l'image du monde extérieur qui permettait de connaître les mouvements de l'avion.
Hélas, on devait manquer d'ergonomes à l'époque, et il faut bien dire que la technique balbutiait encore.
Au lieu d'essayer d'analyser ce qui est utile dans l'information visuelle naturelle afin de la restituer sous une forme instrumentale aussi proche que possible, on s'est orienté vers des instruments donnant des informations abstraites conventionnelles qui demandent à être interprétées pour " matérialiser " mentalement la position et les mouvements de l'avion.
Ce fut 'l'époque héroïque du " P.S.V. " (pilotage sans visibilité). Les " fesses " furent bannies au profit de la Bille, de l'Aiguille et du Badin (le B.A. BA du P.S.V. !) Curieusement, les simulateurs modernes sont dotés de " Motion " : la cabine est animée de mouvements censés reproduire au moins le début des accélérations ; ce qui tend à reconnaître que les sensations ne doivent pas être complètement négligées.
L'évolution des instruments de bord.
La Bille, l'Aiguille et le " Badin " (du nom du constructeur français de l'indicateur de vitesse) ont gardé de leur caractère quasi sacré de jadis un droit imprescriptible à figurer sur les planches de bord.
Pourtant, la bille n'est plus guère utilisée que dans les cas de dissymétrie, car elle se tient pratiquement seule au milieu sur les avions modernes.
L'aiguille est toujours là, mais souvent reléguée dans un coin, comme une chère vieille chose...
Le " Badin ", lui, est resté un instrument essentiel. Permettez-moi de me demander pourquoi, En effet, il n'indique généralement pas la vitesse, mais ce que serait celle-ci... si l'avion volait, sans vent, à l'altitude zéro d'une atmosphère " standard " idéale. Il n'indique pas non plus la portance de l'aile, car on sait fort bien que cette portance est caractérisée par l'incidence, et que la vitesse à laquelle une incidence donnée est obtenue dépend du poids et de l'accélération. Par exemple, une " ressource " brutale à vitesse très élevée peut amener un décrochage de l'aile... que par tradition on continue d'appeler " perte de vitesse ". Je ne vais pas entreprendre une fastidieuse revue critique des instruments de bord classiques : ils sont trop connus.
La preuve de leur insuffisance est démontrée par l'observation qu'ils ne permettent pas, habituellement, à un pilote de se poser avec leur seule aide, alors qu'il le fait à vue malgré certaines lacunes notoires de l'information visuelle que nous examinerons plus loin.
L'explication de l'insuffisance des instruments classiques tient à plusieurs causes :
- La nature des informations fournies n'a, en général, aucun rapport avec celle des références visuelles remplacées.
Par exemple, à vue, la vitesse de virage est indiquée par la vitesse de défilement des repères extérieurs parallèlement à l'horizon, tandis que l'aiguille de l'instrument se déplace d'une quantité qui varie linéairement avec la vitesse de virage autour de l'axe de lacet de l'avion, lequel ne coïncide pas avec l'axe de la trajectoire de virage. Seul l'horizon artificiel se rapproche, par sa nature, de l'information extérieure. En effet, sa " barre " reste parallèle à l'horizon vrai, et la " maquette " est fixe par rapport à l'avion. Mais la taille réduite de l'instrument et l'obligation de baisser les yeux pour l'observer nécessitent une certaine éducation des réflexes qui ne sont pas aussi " naturels " que l'on pourrait croire. Je n'en veux pour preuve que l'existence sur le marché de l'aviation légère d'instruments tels que le " Turn Coordinator " de Brittain, ou encore l'" Attitude Orienter " dans lesquels c'est la maquette qui est mobile sur un fond simulant un paysage fixe par rapport à l'avion., Reconnaissons cependant que l'horizon artificiel a été et reste la base du pilotage sans visibilité.
- La valeur angulaire des déplacements des divers repères instrumentaux est beaucoup plus faible que celle dont semblent se déplacer les images du monde extérieur pour un mouvement donné de l'avion. Le seuil de perception de ce mouvement est donc beaucoup plus tardif dans le cas du vol aux instruments,
- Enfin certaines informations simples ne sont connues que par un calcul résultant d'une combinaison de données fournies par plusieurs instruments (qu'ils soient disséminés sur la planche de bord ou regroupés sur un même cadran).
Les insuffisances du vol à vue.
Il est bien connu que l'information visuelle seule ne suffit pas et qu'en général le pilote la complète par la lecture de ses instruments. Par exemple, la vue extérieure permet de détecter avec précision toute variation d'attitude, mais ne peut en donner une mesure comme le fait un horizon artificiel pourtant dix ou quinze fois moins sensible. Certaines données, telles que la vitesse ou l'altitude, ne peuvent être connues, par la vue extérieure seule, que de façon subjective ou très approximative.
En ce qui concerne le guidage vers une piste et I'atterrissage, il est prouvé que les informations instrumentales seules sont insuffisantes (les systèmes d'atterrissage automatique les plus perfectionnés exigent toujours un contrôle visuel à la hauteur de décision). Par contre, l'expérience montre que tout pilote de ligne sait atterrir sans autre moyen de guidage que l'image de la piste, même s'il n'en voit émerger de la nuit noire que le balisage.
Nous voici ramenés à la cueillette des olives : pourquoi ce qui est si difficile lorsqu'on ne dispose que d'instruments classiques (et si difficile aussi pour un pilote automatique) est-il si simple et évident pour un pilote qui voit cette piste ?
La réponse est digne de Jacques de Chabannes (accessoirement seigneur de La Palisse !) :
" C'est que l'image de la piste, vue par le pilote, contient tout ce qui est nécessaire pour le guider. "
Il reste donc à se donner la peine d'analyser comment une image aussi simple peut " tout " contenir.
Observons d'abord que cette image, comme celle de n'importe quel repère fixe au sol, permet de juger des mouvements de l'avion en tangage et en lacet : toute amorce d'embardée est immédiatement perçue, et ceci est une aide précieuse pour pallier l'imprécision des instruments.
Etudions maintenant comment un pilote peut aligner son avion sur l'axe de la piste d'une part, et sur une pente de descente menant à un point choisi d'autre part.
Guidage visuel en azimut.
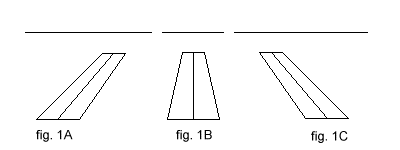
L'il étant plus haut que le plan de la piste, l'axe de celle-ci apparaît comme un segment de droite. Le critère d'alignement est tout simplement la verticalité apparente de ce segment.
Les trois croquis précédents en disent plus long qu'un discours (fig. 1),

Il est évident que l'observateur est à droite de la piste vue en fig. 1A, qu'il est sur l'axe fig. 1B et à gauche fig. 1C.
Si l'horizon n'est pas visible, ou s'il ne peut être remplacé par des repères horizontaux et perpendiculaires à l'axe (tels que seuil de piste, barrettes, " cross-bars ", etc.), il y aura confusion entre roulis de l'avion et écart latéral. Ceci explique pourquoi l'alignement est difficile quand on n'a pas de référence d'horizon ou de ligne d'approche et que le seuil de piste constitue un repère trop petit pour apprécier avec assez de précision- sa perpendicularité avec l'image de l'axe de piste. Mais au fur et à mesure que l'image grossit, les parties horizontales sont de mieux en mieux visibles et l'alignement devient facile.
Cependant, la taille des repères horizontaux n'est pas le plus important. Il faut surtout observer que la sensibilité du guidage croît en raison inverse de la hauteur. C'est ce qui explique pourquoi tout pilote est capable de poser sa roue de nez sur la ligne axiale de la piste, même s'il n'était pas bien aligné pendant son approche. Considérons les deux croquis de la fig. 2 :
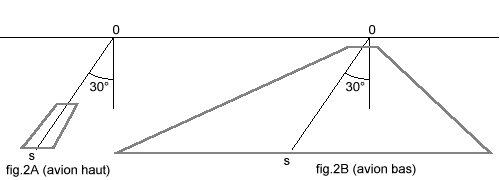
Sur ces deux croquis, la ligne axiale OS, supposée prolongée jusqu'à l'infini sur l'horizon, est inclinée de la même valeur, On voit fig. 2A que cela signifie un écart important, tandis que fig. 2B, cette même inclinaison représente un écart faible. Voyons maintenant ceci de plus près, fig. 3.
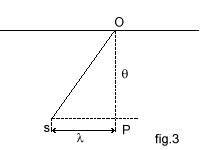
La ligne pointillée passant par OP n'est autre que la trace au sol du plan de l'observateur' Le point O étant sur l'horizon, supposé a l'infini et sur un sol plan et horizontal, SO et PO semblent convergentes sur le dessin, mais peuvent être considérées comme parallèles.
D'autre part, q étant la pente de l'avion, vu du point S, ce point apparaît au même angle q sous l'horizon, ainsi que le montre la fig. 4.
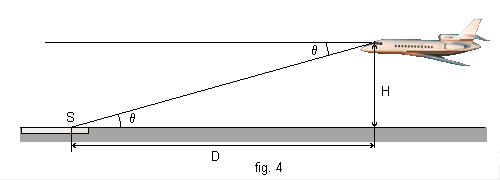
SP représente l'écart latéral du point S avec le plan de l'observateur, ou réciproquement l'écart latéral de l'observateur par rapport au plan vertical contenant l'axe de piste OS (plan du localizer).
Pour les écarts angulaires relativement faibles qui nous intéressent ici (il s'agit de s'aligner sur l'axe, et l'on ne considère qu'un champ limité vers l'avant), l'écart SP vu à une distance D entre l'avion et le point S sous-tend un arc l qui vaut (en radians) :
l = SP / D (1)
La fig. 4 montre que, q étant faible, on peut écrire :
q = H / D (2)
Si l'on se reporte à nouveau fig. 3, on voit qu'on a la relation : tga = l/a
en remplaçant l et q par leurs valeurs tirées de (1) et de (2), il vient :
tg a = SP / D . D/H = SP / H
On voit donc que l'inclinaison apparente de l'axe de la piste par rapport à la verticale est directement proportionnelle à l'écart latéral et à l'inverse de la hauteur.
Pour illustrer ceci, on peut considérer une piste de 45 m de largeur et, par exemple, un écart latéral du quart de cette largeur (avion arrivant au milieu de la bande délimitée par la ligne axiale et un bord de la piste).
On aurait alors
tg a = 11,25 / H
Si l'on fait le calcul pour des hauteurs décroissantes de 1 300 pieds (390 m) correspondant au début d'une approche, jusqu'à 20 pieds (6 m) correspondant à la hauteur de l'il du pilote d un avion de dimension moyenne au sol, on peut dresser le petit tableau suivant :
Tableau I.
Valeur de l'angle a calculé à différentes altitudes pour un écart latéral de 11,25 m.
|
H |
a |
|
1 300' (390m) |
1°,7 |
|
700' (210m) |
3°,1 |
|
300' (90m) |
7°,2 |
|
200' (60m) |
10°,6 |
|
100' (30m ) |
20°,6 |
|
50' (15m ) |
37° |
|
20' (6m ) |
62° |
Si, réciproquement, l'on se fixait une valeur que l'on peut très facilement apprécier, par exemple 5°, on trouverait les valeurs d'écart qui y correspondent (tableau II).
Tableau Il.
Ecart latéral, à diverses altitudes, pour une valeur de a = 5°
|
H |
Ecart |
|
1 300' (390m) |
34.1m |
|
700' (210m) |
18.4m |
|
300' (90m) |
7.9m |
|
200' (60m) |
5.2m |
|
100' (30m ) |
2.6m |
|
50' (15m ) |
1.3m |
|
20' (6m ) |
0.5m |
Ces tableaux confirment que la sensibilité du guidage croît de façon importante au fur et à mesure que l'avion descend, sans pour autant devenir hypersensible puisque c'est ainsi que le pilote est habitué à voir sa piste. Ceci explique l'excellence du guidage visuel en azimut.
Guidage visuel en pente.
La situation est ici nettement moins bonne, bien que l'expérience quotidienne prouve que ce guidage est possible avec la seule vue de la piste,
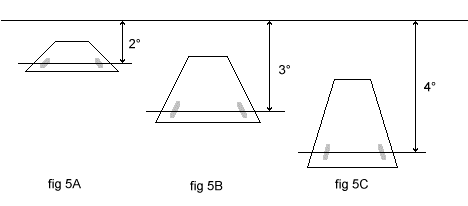
Observons, fig. 5, comment un pilote peut estimer sa pente :
Sur ces trois croquis, où l'avion est supposé à la même distance du point visé (la largeur de piste apparaît sous le même arc), on voit une image de piste d'autant plus " plate " que la pente d'approche est faible. Quand l'horizon n'est pas visible la convergence apparente des bords de piste donne une idée de sa position approximative, et cela reste vrai si l'on ne voit que le début de la piste, le reste étant caché dans le brouillard.
Le point visé (indiqué par deux petits traits de part et d'autre de l'axe) apparaît évidemment à une distance angulaire sous l'horizon qui n'est autre que la pente à laquelle se trouve l'avion, vu de ce point, à l'instant considéré (revoir au besoin la fig. 4).
Dans les cas fréquents où l'horizon est inutilisable, on peut estimer la pente par l'observation du point visé dans le pare-brise : pour une même configuration, une même vitesse d'approche, et un même réglage de siège, ce point doit rester à une même hauteur.
On peut aussi estimer sinon la pente, du moins la trajectoire-sol, en observant le point qui semble immobile dans la direction du vol (certains disent " le point autour duquel grossit l'image "). En effet, seul le point où aboutit la trajectoire semble immobile alors que tous les autres semblent s'en écarter à la façon dont les arbres semblent s'écarter de chaque côté d'une route parcourue à grande vitesse.
La dimension de la piste étant connue, le pilote qui la voit peut estimer grossièrement la distance qui l'en sépare et régler sa descente en conséquence.
Ces procédés " artisanaux " sont évidemment imprécis et c'est la raison pour laquelle ont été implantés au sol des indicateurs visuels d'angle d'approche (V.A.S.I. ou dérivés). Mais ces indicateurs ont leurs limitations et inconvénients sur lesquels je ne m'étendrai pas.
Amélioration du guidage en pente.
il est remarquable de constater que l'un des procédés artisanaux ci-dessus serait excellent... si l'on pouvait être sûr de toujours voir un horizon parfait, et si l'on pouvait afficher, au-dessous de celui-ci, un repère à une distance angulaire égale à celle de la pente choisie.
Or il existe pour obtenir cela un moyen bien connu et bien simple : c'est un collimateur, analogue à un collimateur de tir mais où le réticule classique est remplacé par une image d'horizon.
Les mouvements de cette image sont commandés par un gyroscope de verticale (la même centrale gyroscopique que celle qui alimente l'horizon artificiel classique).
En réglant la sensibilité de cette image de telle sorte qu'elle se déplace de +a° quand l'avion varie de -a° en tangage, on voit une image fixe par rapport au paysage (puisque ce dernier semble aussi se déplacer en sens inverse des mouvements de l'avion).
Le pilote aura donc à sa disposition une image lumineuse d'horizon en coïncidence constante avec l'horizon naturel vrai.
Comme d'autre part il faut pouvoir mesurer l'assiette de l'avion en tangage, l'échelle d'assiette qu'on associe habituellement à l'horizon doit représenter des degrés vrais. L'origine de cette échelle étant évidemment l'horizon vrai, il s'ensuit que le chiffre en regard duquel apparaît n'importe quel repère extérieur vu dans le collimateur indique la valeur de la pente de l'avion, vu de ce point, à l'instant considéré (il suffit encore de se reporter à la fig. 4).
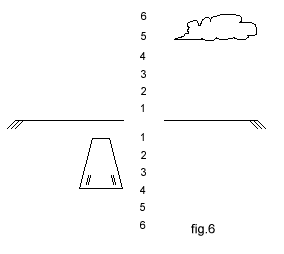
Le pilote voit dans son collimateur une image schématisée par la fig. 6.
Sur cette figure, on voit immédiatement que la pente actuelle de l'avion est de 3° par rapport au point visé (repéré par les deux petits traits de part et d'autre de l'axe de piste), de 3°,5 par rapport au seuil de piste, de 1° par rapport à l'extrémité de piste... et de - 5° par rapport à la pointe gauche du petit nuage !
Voilà un V.A.S.I. embarqué très supérieur à ceux implantés au sol, car il est utilisable pour n'importe quelle valeur de pente et laisse le libre choix du point visé, ce qui élimine le danger d'utilisation des V.A.S.I. classiques par les avions de très grandes dimensions.
On objectera qu'il suffirait pratiquement de faire figurer le chiffre 3 de l'échelle, ou un repère ajustable gyro-stabilisé. Exact. Mais puisqu'il faut un horizon artificiel pour piloter, autant le conserver, d'autant plus que son échelle d'assiette a encore un autre intérêt, ainsi que nous allons le voir.
Le Vecteur-Vitesse.
Le " Badin " traditionnel n'est qu'un moyen indirect, donc, insuffisant, de connaître la portance de l'aile, et nous avons dit qu'il serait bien préférable de lire directement l'incidence.
L'idée, certes, n'est pas nouvelle, mais il y avait quelques difficultés : trouver un détecteur fonctionnant avec une sensibilité et une précision suffisantes, trouver la loi de correction d'installation pour convertir l'incidence " locale " (au point d'implantation du détecteur) en incidence vraie (direction du vent relatif " à l'infini amont "), puis finalement trouver une représentation qui en rende l'utilisation naturelle pour le pilote.
Un ingénieur en chef du Service Technique de l'Aéronautique, M. Klopfstein, a eu le mérite de s'attaquer à l'ensemble du problème et de le résoudre complètement par le calcul et par des essais en vol particulièrement probants.

Considérons la fig. 7, et supposons que l'on sache, au moyen d'une girouette ou sonde appropriée convenablement corrigée, mesurer exactement l'angle i entre le vent relatif et l'axe de référence de l'avion (angle d'incidence).
Le Vecteur-Vitesse n'est autre que le Vecteur Vent relatif inversé de 180°. Sa direction est donc celle de la trajectoire-air de l'avion, c'est-à-dire sa trajectoire géographique en air calme.
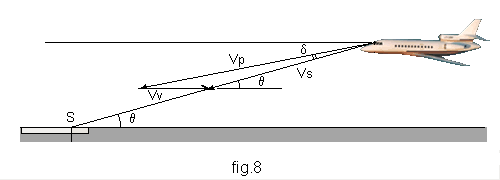
S'il y a du vent, il se produit, dans le plan vertical, une " dérive " analogue à celle observée en navigation classique dans le plan horizontal. Dans le cas d'un vent debout et d'une trajectoire en descente (fig. 8), la trajectoire est déviée vers le bas d'un angle d. Cet angle est la correction dont il faut " relever " le vecteur-vitesse pour suivre une trajectoire géographique q, exactement comme la dérive est la correction à faire subir au cap pour suivre une route.
Le calcul est identique à celui de la navigation classique. On a :
Vv / sind = Vp / sin q d'où sin d = sinq . Vv / Vp
Mais ici les choses sont plus simples qu'en navigation classique, car q est toujours petit (les pentes habituelles de Glide-Path sont de l'ordre de 3°). Aussi peut-on confondre sin et arc et écrire :
d° = q . Vv / Vp
Comme d'autre part le vent moyen en approche n'est connu qu'approximativement, on peut prendre pour q une valeur arrondie à 3° et écrire :
d° = 3 . Vv / Vp
Abandon de l'assiette.
M. Klopfstein a également démontré en théorie et en pratique que le vecteur vitesse est " pilotable " : autrement dit, le manche peut le commander en tangage tout comme l'avion lui-même (ou la maquette, dans le cas d'un horizon artificiel).
Ainsi, en profondeur, on pilote directement la trajectoire, et non plus l'axe de l'avion dont la direction dans le plan vertical ne correspond pas avec celle du vol, puisque précisément la portance exige une incidence !
L'angle d'assiette traditionnel perd donc son intérêt.
Utilisations du vecteur-vitesse.
La simple mesure de l'angle d'incidence et la reproduction dans un collimateur où figure déjà un horizon artificiel de sensibilité 1/1 amène une série de conséquence qui vont rendre les informations de pilotage beaucoup plus complètes et précises tout en les simplifiant considérablement.
Contrôle de la portance.
Il se fait directement par le choix d'une incidence, donc indépendamment du poids (élimination du risque d'erreur dans le calcul des vitesses de référence) et de l'accélération (variable avec l'inclinaison du virage ou qui est incontrôlable quand elle est due à une ressource ou à des rafales), La représentation schématique dans un collimateur est fort simple (fig. 9A).
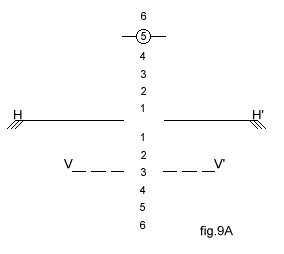
Soit HH' l'horizon, VV' le repère du vecteur-vitesse, et M la maquette. Sur la fig. 9A. la maquette est calée sur l'axe de référence avion. Elle indique la valeur de l'assiette : 5°, qui nous importe assez peu. Le vecteur-vitesse indique une pente descendante de 3°. L'incidence est donc 5 + 3 = 8°. Tout simple que ce soit, il ne serait pas commode d'avoir à faire ce calcul ; aussi puisqu'il s'agit de maintenir un écart constant entre la maquette et le repère VV', il est plus pratique de décaler M vers le bas de l'angle choisi : c'est ce que montre la fig. 9B. Une fois qu'on a affiché l'incidence, piloter celle-ci est, pour un pilote, aussi simple que... de cueillir une olive : si la maquette est vue au-dessus du vecteur-vitesse, c'est qu'on se trouve " nez haut ", donc à incidence plus forte que celle à tenir (et accessoirement vitesse plus faible), et réciproquement si la maquette était vue plus bas que VV'. Les croquis 10A et B illustrent ceci :
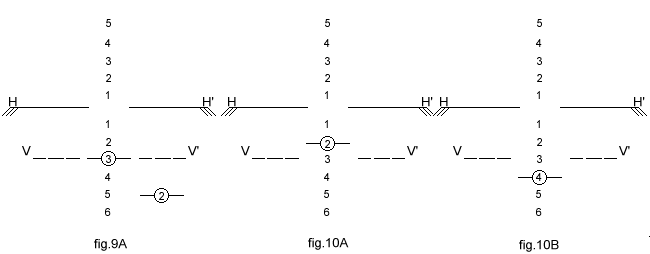
En configuration d'approche, une variation d'incidence de 1° équivaut environ à 5 kt. La fig. 10A montre une incidence trop forte de 1°, donc une vitesse trop faible d'environ 5 kt. C'est évidemment l'inverse fig. 10B. L'expérience montre qu'on peut facilement distinguer un écart inférieur au quart de degré (la moitié du diamètre apparent du soleil ou de la lune), Ceci veut dire qu'on peut apprécier la vitesse au nud près. Si l'on s'est fixé la trajectoire (comme c'est le cas en approche), alors la position relative de la maquette doit se tenir uniquement par action sur les gaz.
Il est amusant de constater qu'en quelques minutes (et même moins d'une minute), le réflexe est acquis : on pousse sur les manettes dès qu'on voit monter la maquette et l'on réduit dès qu'on la voit descendre. Je puis en témoigner pour l'avoir vérifié moi-même au Centre d'Essais en Vol d'Istres, sur un avion que je n'avais jamais piloté.
Pente-air.
Il est évident que le chiffre de l'échelle d'assiette en regard duquel est vu le repère VV' indique directement la valeur de la pente-air, en montée comme en descente.
Vitesse verticale.
Celle-ci est proportionnelle à la pente-air et à la vitesse propre de l'avion. Ceci ne donne pas directement la valeur de la vitesse verticale, mais fournit une indication immédiate de sa variation, ce qui est bien utile connaissant le temps de retard dont est affligé le variomètre classique.
Trajectoire.
Le vecteur-vitesse indiquant la direction de la trajectoire-air, il est évident que le point du sol aperçu en regard du repère VV' est celui où arriverait l'avion si les conditions restent stables. Si le pilote maintient par action sur le manche le repère VV' sur un point déterminé de la piste, sa trajectoire y aboutira, même s'il y a du vent et qu'il ne le corrige pas : l'avion décrira alors une sorte de " courbe du chien " dans le plan vertical. Dans le cas le plus fréquent d'une approche vent debout, la courbe " creuse " au-dessous de la pente rectiligne idéale (fig. 11).
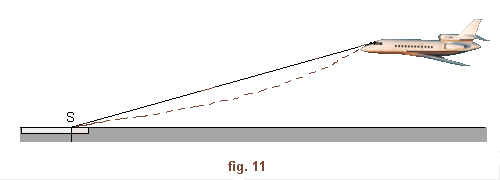
Le calcul et l'expérience montrent que le " creux " est faible et peut être négligé dans la plupart des cas. Mais rien n'empêche de faire la correction par la formule approchée indiquée plus haut :
d° = 3 . Vv / Vp
Il est important de ne pas oublier le juge de paix... c'est-à-dire l'horizon, dont l'échelle d'assiette permet un contrôle continu de la pente. Supposons que le pilote n'ait pas corrigé, ou qu'il n'ait pas assez corrigé un vent debout : sa trajectoire va passer sous le plan de descente prévu. Donc le point visé semblera monter au-dessus de la valeur de pente choisie. Il suffira au pilote de viser un peu plus haut jusqu'au moment où il verra la pente revenue à la valeur correcte.
Gradient de vent.
Supposons un avion approchant vers une piste, et soumis en altitude à un vent de face important. Sa vitesse par rapport au sol est diminuée de celle du vent : elle est donc " faible ". Si le vent décroît au fur et à mesure de la descente, l'avion tend, par inertie, à conserver cette vitesse faible, mais comme le vent relatif a diminué, il faut plus d'incidence pour conserver la portance. La trajectoire de descente s'accentue donc, aggravant le phénomène puisque le vent va décroître encore plus vite ! Ce gradient est responsable de nombreux accidents par impacts avant la piste.
Avec des instruments classiques, le pilote n'a aucun moyen de s'apercevoir à temps du phénomène : il n'a pas de contrôle précis de pente et le premier avertissement vient en général de son Badin qui régresse, puis vient l'indication du variomètre qui indique une vitesse de chute excessive. La poussée des réacteurs est souvent insuffisante à ce moment pour corriger, et la seule action efficace est de redresser la pente en espérant que la réserve de vitesse le permettra encore.
Mais observons ce qui se passe quand on utilise un vecteur-vitesse dans un collimateur : dès que l'incidence augmente, le repère VV' a tendance à descendre sous le point visé. Comme le pilote s'appliquait à maintenir VV' sur ce point, il tirera presque inconsciemment sur le manche et maintiendra ainsi sa trajectoire. Simultanément, le pilote ayant tiré sur le manche verra la maquette " monter " au-dessus du repère VV' et, par réflexe, poussera sur les manettes de gaz. Ainsi ses deux actions seront correctes, immédiates... et aussi instinctives que pour faire le geste de cueillir une olive 1 Voilà une solution particulièrement élégante à un problème qui fait encore pâlir de nombreux experts dans des réunions internationales.
Dispersion des atterrissages.
Le vecteur-vitesse a permis de mettre au point le principe d'une méthode réduisant considérablement la dispersion des impacts à l'atterrissage.
L'approche se fait comme indiqué ci-dessus en maintenant le repère VV' sur le point visé de la piste, puis, à une certaine hauteur (lue par exemple au radioaltimètre, et variable avec le type d'avion) on relève le vecteur-vitesse d'un certain angle, par exemple de 3 à 1°, jusqu'au contact des roues. Les valeurs sont déterminées expérimentalement de façon à obtenir un contact avec le sol franc, sans être dur. Les essais menés jusqu'à présent montrent une dispersion remarquablement faible.
Pente potentielle.
On sait que, partant d'une condition de vol stable, toute variation de pente produit une accélération ou une décélération. Réciproquement, toute accélération ou décélération produite par une modification de la poussée peut être transformée en pente équivalente, en maintenant la vitesse initiale.
Mon ami Georges Carmeille avait fait le calcul exact de l'énergie potentielle d'où il avait tiré la " recette " bien connue de ses élèves :
+- 1% de pente = +- 0,2 kt/sec.
Pour ceux que rebuterait le calcul de l'énergie potentielle, on peut expliquer ceci aussi simplement que pour une bille sur un plan incliné. Partant de conditions stables en vol horizontal, si l'avion prend une pente de 1%, une composante égale à 1% de son poids va s'appliquer à sa masse M et, en vertu du principe fondamental de la mécanique, va lui communiquer une accélération :
g = f / M = P / 100M = Mg / 100M = g / 100 @ 0,1 m/sē
en arrondissant g à 10 m/secē au lieu de 9,81 m/secē et comme 1 M/Sec = 2 nuds, on retrouve la formule de Carmeille puisque 0,1 m/secē = 0,2 kt/sec.
Bien entendu, ceci n'est vrai que tant qu'il est possible de considérer que la poussée et la traînée n'ont pas varié, donc que la vitesse est restée pratiquement la même. Or c'est justement ce qui nous intéresse ici: il s'agit de connaître quelle pente est " permise ", avec une poussée disponible, sans altérer la vitesse.
M. Klopfstein - encore lui ! - a eu l'idée de placer dans un collimateur un repère à la valeur de cette pente qui permet d'annuler l'accélération. Il a mis au point un système simple et astucieux pour mesurer correctement cette accélération et la traduire en valeur de pente.
L'utilisation est remarquablement facile : il suffit de piloter le vecteur-vitesse pour l'amener en face de ce repère de pente. L'intérêt en cas de remise de gaz avec panne de moteur est évident, car le pilote peut prendre immédiatement la pente optimum qui lui permet de conserver sa vitesse. A l'inverse, si l'on se fixe une valeur de pente, on peut immédiatement ajuster la poussée à la valeur nécessaire pour conserver la vitesse ou, plus exactement, l'incidence choisie.
L'atterrissage " tous temps ".
Il semble que nous ayons davantage discuté d'olives que d'atterrissages tous temps. Pourtant, il n'en est rien :
L'expression tous temps étant tirée de l'anglais " all weather " dit bien qu'il s'agit d'atterrissage par tous les types de temps. il ne faudrait pas, pour régler le problème de la minorité des atterrissages dans le brouillard. négliger les besoins de la " majorité silencieuse ", composée de ces milliers d'atterrissages pratiqués de jour et de nuit dans des conditions que l'on est convenu d'appeler " à vue ", et dont il faut bien dire qu'on ne s'était guère préoccupé jusqu'à présent.
Je pense que les moyens très simples indiqués plus haut : horizon, vecteur-vitesse, pente potentielle, fournis dans un collimateur, seraient de nature à combler tous leurs besoins,
Restent ceux spécifiques des atterrissages par visibilité réduite ou nulle.
Or nous avons vu que l'image naturelle de la piste avait des vertus remarquables en ce qui concerne le guidage en azimut, et quelques insuffisances en ce qui concerne le guidage en pente, mais que celles-ci pouvaient être corrigées par les moyens indiqués.
Piste artificielle.
La conclusion logique vient d'elle-même il faut placer dans le collimateur une image artificielle schématisant l'essentiel de l'image de la piste naturelle, et qui lui soit superposable, L'image serait utilisable d'instinct " comme la vraie piste " et dispenserait de tout directeur de vol.
Au lieu d'utiliser les signaux de l'ILS pour commander des déplacements d'index ou d'aiguilles peu exploitables par le pilote, il serait plus judicieux de s'en servir pour construire dans le collimateur une image telle que le simple segment OS de la fig. 3. L'inclinaison de ce segment serait commandée par les signaux du localizer (corrigés du décalage entre la position des antennes et le point visé, grâce à une formule simple traitée par un petit calculateur de bord), et la position du point S à l'angle q serait fixée directement par les signaux d'écart du glide-path après affichage de la pente de l'ILS utilisé.
Cependant, la fig. 2 avait montré qu'une même inclinaison apparente de l'axe signifie un écart important lorsqu'on est haut, ou faible quand l'avion arrive sur la piste. Sans doute le pilote connaît son altitude, et peut ainsi doser l'amplitude de ses corrections. Mais cela n'est guère commode, et mieux vaut continuer à réunir les conditions pour que le pilote agisse simplement, par réflexe, comme en vol à vue.
Or il se trouve que pour des préoccupations de fiabilité, on a trouvé peu raisonnable de faire reposer la sécurité du vol sur le seul ILS (le pilote ne pouvant intervenir que par un contrôle visuel extérieur pour décider au dernier moment s'il peut continuer l'atterrissage ou remettre les gaz).
Aussi des recherches sont-elles entreprises pour mettre au point un ILM (Independent Landing Monitor) qui fournirait, à partir d'un radar de bord, les écarts de l'avion avec l'axe de la piste et avec le plan de descente. Les signaux obtenus seraient alors envoyés conjointement à ceux de l'ILS dans un comparateur d'où sortiraient, en cas de désaccord, des signaux d'alarme.
Mais l'ILM donne un " sous-produit " intéressant : c'est la possibilité de fabriquer une image de piste, par ailleurs indispensable pour un instrument de bord électronique, l'EADI (Electronic Attitude Director Indicator), en cours de mise au point pour rassembler les informations éparses sur les planches de bord classiques.
Cette image radar, qu'elle soit obtenue directement pour elle-même, ou en sous-produit de l'ILM, viendrait donc doubler fort utilement l'images ILS.
Si l'on utilise l'image radar pour représenter les bords de piste, et l'image ILS pour représenter la ligne axiale, ainsi qu'on le voit par exemple sur les figures 2A ou 2B, alors il est évident que le pilote n'a besoin d'aucun comparateur : c'est aussi simple que de cueillir une olive !
Tant que la ligne axiale est au milieu de l'image des bords et que la base des deux images est à la même distance angulaire sous l'horizon, c'est que les deux moyens de guidage sont d'accord... et l'atterrissage peut se poursuivre en sécurité, même si l'on ne voit pas la piste réelle prendre le relais en se superposant aux images artificielles. On notera aussi que c'est l'image radar seule qui donne la notion de largeur de piste, si commode pour doser les corrections ; toutefois ceci étant davantage une affaire de confort de pilotage que de sécurité, il n'est pas indispensable de demander aussi cette information à l'image ILS (cela serait possible par un segment horizontal passant par le point S).
Il est à remarquer également que l'image du seuil de piste fournie par l'image radar peut, dans une certaine mesure, doubler l'horizon artificiel à très basse altitude.
Conclusion.
La solution d'ensemble préconisée relève d'une philosophie fort différente de celle qui prévaut depuis plusieurs années.
Elle est évidemment combattue par ceux qui ont misé sur un automatisme intégral, nécessitant des protections coûteuses par redondance et sécurités automatiques diverses.
Il n'est fait appel ici qu'à une technologie très simple et bien au point : reproduction d'angles, positionnement de l'image à partir des signaux de l'ILS.
Cependant, il faut encore attendre le résultat des travaux, actuellement en bonne voie, pour savoir si l'on pourra obtenir une image radar fiable et économique. (Il y a bon espoir de pouvoir utiliser partiellement l'équipement radar météo.)
A ce moment, le système complet aura sur les systèmes automatiques les plus raffinés l'énorme avantage d'un guidage non visuel par deux moyens distincts et indépendants, mais présentés au pilote sous une forme exactement semblable à celle qu'il a l'habitude d'utiliser à vue.
Ainsi, quelles que soient les conditions de visibilité, donc par " tous temps ", il travaillera avec les mêmes références, les mêmes instruments et les mêmes méthodes, ce qui est le meilleur gage de ce que nous poursuivons tous avec acharnement : la sécurité.
René LAMI.
Février 1971.